6552. Время жить
Как Вы
знаете, большинство компьютерных сетей имеют древовидную структуру, то есть от
каждого и до каждого компьютера можно добраться только по единственному пути.
Так
называемый параметр Время Жизни (ВЖ) определяет количество шагов, через которое
блуждающий по сети пакет данных уничтожается, если он еще не достиг места
назначения. Цель ВЖ состоит в том, чтобы избежать бесконечной циркуляции по
сети, вызванной ошибками в таблицах маршрутизации.
Размещение
маршрутизатора, соединяющего одну сеть с другой, считается оптимальным, если
максимальное необходимое ВЖ для пакетов, отправляемых с этого маршрутизатора на
другой компьютер в той же сети, минимально. По заданной сети Вам следует
рассчитать для нее максимальное значение ВЖ, если Вы сами можете выбрать
компьютер, который следует использовать в качестве маршрутизатора.
Вход. Первая
строка содержит количество тестов c
(1 ≤ c ≤ 100). Первая
строка каждого теста начинается с количества компьютеров n (1 < n ≤ 105)
в сети. Компьютеры пронумерованы числами от 0 до n – 1. Каждая из следующих n
– 1 строк описывает двунаправленное соединение между компьютерами a и b
(0 ≤ a, b < n).
Выход. Для каждого теста выведите в отдельной строке
оптимальное значение ВЖ.
|
Пример входа |
Пример выхода |
|
3 2 1 0 5 3 2 2 1 0 2 2 4 9 3 1 6 5 3 4 0 3 8 1 1 7 1 6 2 3 |
1 1 2 |
РЕШЕНИЕ
графы – поиск в глубину
Анализ алгоритма
В центре
заданного дерева следует поставить маршрутизатор, так как именно от него
расстояние до самой дальней вершины минимально. Если d – диаметр дерева, то расстояние от его
центра до самой дальней вершины равно ![]() .
.
Диаметр
дерева ищем поиском в глубину (или в ширину). Первым поиском в глубину найдем кратчайшие
расстояния от вершины 0 до всех остальных. Найдем вершину v, самую отдаленную от 0. Запустим
второй поиск в глубину из вершины v. Расстояние
от нее до самой дальней вершины равно диаметру d дерева.
Пример
Рассмотрим деревья, приведенные в
тестах. Выделенная вершина – центр
дерева.
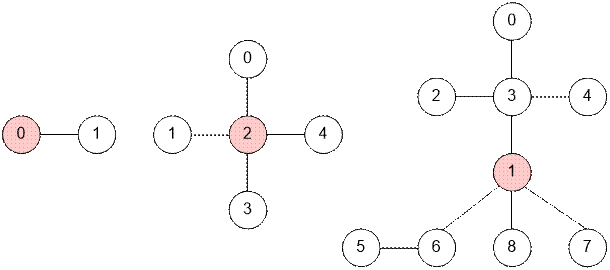
Реализация алгоритма
Дерево в
виде списка смежностей храним в массиве g. Объявим массив кратчайших расстояний
dist.
vector<vector<int> > g;
vector<int> dist;
Функция
dfs совершает поиск в глубину из вершины v. Предком v является prev. Кратчайшее расстояние от стартовой вершины до v равно d.
void dfs(int v, int prev = -1, int d = 0)
{
dist[v] = d;
Перебираем
сыновей вершины v. Рассматриваем
ребро v → to.
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
Если to не является предком v, то запускаем поиск в глубину из
вершины to. Расстояние от стартовой вершины до to равно d + 1.
if (to == prev) continue;
dfs(to, v, d + 1);
}
}
Основная
часть программы. Читаем входные данные.
scanf("%d", &tests);
while (tests--)
{
scanf("%d", &n);
g.clear();
g.resize(n);
for (i = 0; i < n - 1;
i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
dist.clear();
dist.resize(n);
Ищем самую
дальнюю вершину v от нулевой.
dfs(0);
v = max_element(dist.begin(), dist.end()) - dist.begin();
Ищем самую
дальнюю вершину u от v.
dfs(v);
u = max_element(dist.begin(), dist.end()) - dist.begin();
Значение
dist[u] равно диаметру дерева. Расстояние от центра дерева, где
расположен маршрутизатор, до самой отдаленной вершины составляет ![]() .
.
printf("%d\n", (dist[u] + 1) / 2);
}
Реализация через поиск в глубину
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace
std;
vector<vector<int>
> g;
int diameter, i, n, u, v, tests;
int dfs(int
v, int prev = -1)
{
int h1 = 0, h2 = 0; //
highest and second highest height
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i];
if (to != prev)
{
int h = dfs(to,v) + 1;
if (h > h1) h2 = h1, h1 = h;
else if (h > h2)
h2 = h;
}
diameter =
max(diameter, h1 + h2);
}
return h1;
}
int main(void)
{
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
g.clear();
g.resize(n+1);
for(i = 0; i < n - 1; i++)
{
scanf("%d %d", &u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
diameter = 0;
dfs(0);
printf("%d\n",(diameter+1)/2);
}
return 0;
}